54화 : 수학 논문과 저자권

오늘은 미국 독립기념일이니 독립사건에 대해서 짧게.

여기 확률 공간이 있음

여기에 이제 두 독립 사건을 그려볼 것임. 답을 보여주기 전에 한 번, 어떻게 그리는 것이 올바를지 생각해보길

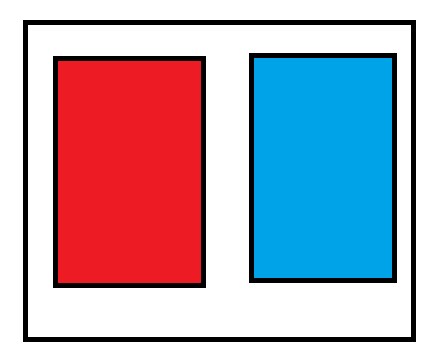
만약

이렇게 그렸다면, 아쉽지만 오답임.

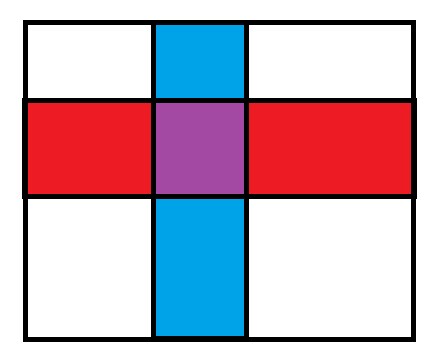
정답은

이렇게 그려야 함. 보라색 부분은 두 영역의 교집합으로, 두 사건에 모두 포함되는 부분임.

사람들이 두 사건이 독립적이라는 말을 들으면 아무래도 겹치지 않고 서로 떨어져 있는 상황을 상상하기 쉽지만, 얼핏 생각되는 직관과 반하게 그려지게 되고, 이는 실제로 확률론의 역설들에 적지 않은 영향을 끼치지 않을까 싶기도 함.

맨 처음 그림이 오답이 되는 이유는, 빨간 사건이 일어난다면 파란 사건이 절대로 일어나지 않는다는 사실이 보장되기 때문임. 따라서, 파란 사건은 빨간 사건에 종속적임. 빨간 사건의 정보만으로 파란 사건의 여부를 어느 정도 파악할 수 있기 때문. 잘 생각해보면 서로 상관이 없다는 것과 서로 배타적이라는 것은 모순적이기도 함.

다시말해, 진짜 대락적으로 말하자면, 확률론에서 독립성은 "여부의 독립성"이 아닌, "정보의 독립성"임.

실제로 확률을 다루다보면 A와 B가 독립이고, B와 C가 독립이고, A와 C가 독립이라면 A,B,C 가 모두 독립적이다! 같은 오류를 범하기 쉬운데, 이 또한 위쪽 독립성과 연관이 있음. 독립에 대한 이미지가 첫 그림과 같다면 이 내용이 참이 되기 때문.

하지만 실제로는, A와 B, B와 C, C와 A가 서로 독립이라고 해도 셋을 모으면 독립이 아니게 될 수 있음. A 단독, 혹은 B 단독이라는 정보만으로는 C를 전혀 파악할 수 없지만 A와 B가 합쳐지면 C가 유추 가능한 경우는 흔하기 때문임.

대표적으로 동전을 두 번 던진다고 했을 때, A는 첫 번째가 앞면이 나오는 사건, B는 두 번째가 앞면이 나오는 사건, C는 두 번 던진 결과가 같은 사건이라고 하면, A와 B, B와 C, C와 A는 서로 독립임. 하지만 A, B 사건에 관한 정보를 둘 다 파악하고 있다면, 우리는 C에 대해서는 완전히 결정적인 결론을 내릴 수 있고, 따라서 A, B, C 모두는 독립이 되지 않음.

그리고 사실 이러한 직관은 선형대수학에서 나오는 선형 독립과도 조금 연관이 있음. 위의 정답 그림에서 보듯, 독립적인 사건은 어떤 관점에서 보면 축에 해당되는 사건임. x축과 y축이 서로 독립적인 것처럼. 즉, 두 사건이 독립적이라는 것은 어찌보면, 두 사건이 일종의 "사건 평면"을 만드는 것과 비슷한 느낌이 있음.

즉 A, B, C가 둘 씩은 서로 독립이지만 셋 모두를 모으면 독립이 되지 않는 상황은 A, B가 만드는 "사건 평면"에 C라는 사건이 완전히 들어가는 경우랑 비슷한 느낌인 셈. 위의 동전 예시를 선형대수학적으로 생각하자면, A는 x축, B는 y축, 그리고 C는 y=x라는 직선처럼 생각할 수 있음. A와 B, B와 C, C와 A는 모두 xy평면을 만드는 좌표축으로 사용할 수 있지만 여기서 둘을 고르면 남은 하나는 새로운 축으로 작동할 수 없게 됨.

물론 확률 공간은 선형 공간보다 훨씬 자유롭기 때문에 모든 확률 공간을 이렇게 기하학적으로 이해할 수는 없음. 하지만 직관을 얻는 데는 이런 기하학적 이해가 조금은 도움이 될 지도 모름.

1. 확률론은 생각보다 직관에서 벗어나는 경우가 튀어나온다.

2. 기하학적 직관은 수학을 이해하는 데 많은 도움을 준다.

3. 그렇다고 모든 것을 기하학적으로 이해할 수 있는 것도 아니므로 잘 파악하자.